clique-based abstraction

PRA* (clique-based abstraction) mapping

---

(a) Apply the clique-based abstraction used in PRA* to the graph below. For this, scan the nodes from top-left to bottom-right - row by row, identifying new maximum size complete subgraphs of size up to 4 that can be abstracted into new nodes in the next abstraction level - starting from the current node and scanning its unvisited neighbourhood. Continue this process until only one node remains, showing the resulting abstraction levels and indicating which nodes got abstracted by what node in the process. Use uppercase letters A,B,C,… to name new abstract nodes and explain all steps.

A: {a,b} B: {c,d} C: {e,f} D: {g,n}

E: {h,i} F: {j,k} G: {l,m}

H: {o,p} I: {q,r} J: {s,t} K: {u}

• Step 1

  Starting from the top-left nodes, I consider nodes {a, b}. They are connected and form a complete subgraph of size 2. I can abstract this subgraph into a new node A.

  Before going to the next step, I need to check if A is the maximal clique (Is it possible to increase the size?). I can do this by checking the neighbors of a and b. {c} is a neighbor of b and {h} is a neighbor of a. I can add h to the subgraph. I could try to add c, h, or both to the subgraph, and check if the subgraph is still a clique.

  Any nodes from a subgraph have to be adjacent. However, Any additional node would break the clique property. Therefore, the maximum size complete subgraph of size up to 4 is {a, b}. I can abstract this subgraph into a new node A.

  I continue the same process for the next complete subgraph. At the end of the first row, I have node {g}. I already know the previous nodes are not supposed to be grouped with g. I can add n to the subgraph. The maximum size complete subgraph of size up to 4 is {g, n}. I can abstract this subgraph into a new node D.

  I continue scanning the nodes on the second row. On the second row, I don’t need to consider the node n because it is groupped with the node g from the first row.

  I continue the same process for the last row. At the end of the last row, I have node {u}. I can not add another node to the subgraph. The maximum size complete subgraph of size up to 4 is {u}. I can abstract this subgraph into a new node K.

  I connect the abstract nodes with the edges of the original nodes. I can see that the abstract nodes preserve the connectivity of the original graph.

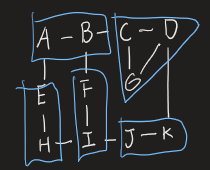
L: {A,B} M: {C,D,G} N: {E,H} O: {F,I} P: {J,K}

• Step 2

  The same logic is applied here. Starting from the top-left nodes, I consider nodes {A,B}. They are reduced to L. I move to {C}. However, C is connected to D and G making a complete subgraph of size 3. I can abstract this subgraph into a new node M.

  I continue the same process for the next row. As you can see above, I can group the nodes {E,H} into a new node N. I can group the nodes {F,I} into a new node O, and the nodes {J,K} into a new node P.

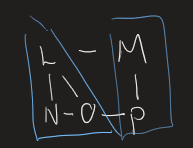
Q: {L,N,O} R: {M,P}

• Step 3

  It becomes easier and easier as I go on. I consider the nodes {L,N,O}. They are a complete subgraph of size 3, and I reduce them into a new node Q. Finally, the nodes {M,P} become a new node R.

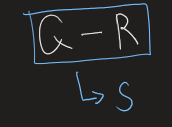
S: {Q,R}

• Step 4

  The last step is to group the nodes {Q,R} into a new node S, and then I am done with the abstraction process.

---

(b) Assuming the original graph size is \(N = 4^n\) and clique-based abstraction being able to always group 4 nodes to form a new abstract node in each step:

1. how many nodes does the \(k-th\) abstraction level consist of (k = 0: original graph with \(4^n\) nodes, k = 1: first abstraction level with ? nodes, etc.)?

   At abstraction level k = 0, the original graph has \(4^n\) nodes. At abstraction level k = 1, the number of nodes is \(4^{n-1}\).

   At abstraction level k = 2, the number of nodes is \(4^{n-2}\).

   At abstraction level k = 3, the number of nodes is \(4^{n-3}\).

   At abstraction level k = n, the number of nodes is \(4^{n-n} = 4^0 = 1\).

   Therefore, the number of nodes at the k-th abstraction level is \(4^{n-k}\).

2. which abstraction level contains exactly one node? Explain

   The abstraction level k = n contains exactly one node.

   This is because at each abstraction level, the number of nodes is divided by 4.

   Therefore, at the n-th abstraction level, the number of nodes is \(4^{n-n} = 4^0 = 1\).

3. assuming we reach one node at abstraction level n = 2u for an integer u, how many nodes does abstraction level u consist of in relation to the original number \(N = 4^n\)? Simplify your answer and explain your steps

   If I reach one node at abstraction level n = 2u for an integer u,

   the number of nodes at abstraction level u in relation to the original number \(N = 4^n\) is \(4^{n-u} = 4^{2u-u} = 4^u\).

   I know n = 2u and \(4 ^{n-2u} = 4 ^{0} = 1\).

   \[\frac{4^n}{4^{2u}} = 4 ^{n-2u} = 1\]

   I can find the number of nodes at abstraction level u:

   \[4^{n-u} = 4^{2u - u} = 4^u\]

   Thus, the number of nodes at abstraction level u in relation to the original number \(N = 4^n\) is \(\sqrt(N)\).

4. Prove that the clique abstraction used in PRA* preserves connectivity, i.e., given A,A′ and B,B′, where A′ is the abstract node for A and B′ is the abstract node for B, there is a path from A to B in the original map if and only if there is a path from A′ to B′ in the abstract map. Note: your proof needs to show both implication directions.

• A, B -> A’, B’

  A’ is the abstract node for A and B’ is the abstract node for B.

  This means that A is in a subgraph (-> A’) and B is in another subgraph (-> B’).

  If there is a path from A to B in the original map, then there is a path from a subgraph (-> A’) containing A to a subgraph (-> B’) containing B.

  Thus, there is a path from A’ to B’ in the abstract map.

• A’, B’ -> A, B

  If there is a path from A’ to B’ in the abstract map, then there is a path from a subgraph containing A to a subgraph containing B.

  However, A is in a subgraph (-> A’) and B is in another subgraph (-> B’).

  Thus, there is a path from A to B in the original map.

• Conclustion

  Therefore, the clique abstraction used in PRA* preserves connectivity.