building pyramids - kattis

Attemp to mathematically approach to the question

Question

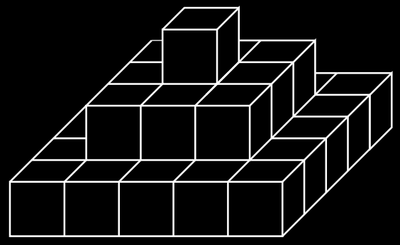
Figure 1: An example pyramid of height 3 with 35 blocks from kattis.

When initiating a larger project, like building a pyramid, it’s best to think twice. Your task today is to write a program that computes how high a pyramid can be built given a certain number of blocks of stone.

We assume that the pyramid to be built is compact, i.e. there are no cavities inside. Furthermore, we assume it is built according to the principle in Figure 1. Each layer is square, with a side length that is two less than the one below it. The top layer always consist of a single block.

It is fine if you have leftover blocks, as long as you build a complete pyramid.

Input

$$ 1 \leq N \leq 10,000,000 $$

Output

$$ \text{Number of layers} $$

 

Sample Input

$$ 83 $$

Sample Output

$$ 3 $$

Mathematical Approach

1st layer has 1 block
2nd layer has 9 blocks
3rd layer has 25 blocks

It seems like there is a pattern.
The number of blocks for (k + 1)-th layer follows formula (2k + 1)2 where k ≥ 0, k is Natural Number.


Click here to example

To find the number of blocks in the 4th layer:

Let k = 3 (since the 4th layer corresponds to k = 3).

Using the formula:

Number of blocks = (2 × 3 + 1)2 = 72 = 49

Thus, the number of blocks for the 4th layer is 49 blocks

Let’s make this more clear!

The number of blocks in the \((k+1) \text{-th layer }\) is given by:

\[\text{Number of blocks} = (2k + 1)^2 \quad \text{where } k \in \mathbb{N}\]

Now all I have to do is calculate the number of blocks for each layer. As long as the sum of blocks from each layer is not beyond the given number of blocks, it continues.

This was not too hard…

And this came to my mind… Maybe there is a way to know how many layers I can build without calculating from the 1st layer.

After the first layer, each subsequent layer contains all the blocks from the previous layer plus additional blocks.

I can write this as below

\[\sum_{i=0}^n \left( 1 + 8 \cdot \left( \sum_{j=0}^i j \right) \right)\]
\[\begin{align*} \sum_{i=0}^n \left( 1 + 8 \cdot \left( \sum_{j=0}^i j \right) \right) &= \sum_{i=0}^n \left( 1 + 8 \cdot \left( \frac{i \cdot (i+1)}{2} \right) \right) \quad\\ &= \sum_{i=0}^n \left( 1 \right) + 4 \cdot \sum_{i=0}^n \left( i^2 \right) + 4 \cdot \sum_{i=0}^n \left( i \right) \\ &= (n + 1) + 4 \cdot \frac{n \cdot (n + 1) (2n + 1)}{6} + 4 \cdot \frac{n \cdot (n + 1)}{2} \\ &= \frac{1}{3} \cdot \left( 4n^3 + 12n^2 + 11n \right) + 1 \\ \end{align*}\]
Click here for details

\(\sum_{k=1}^n k = 1 + 2 + 3 + \dots + n = \frac{n \cdot (n+1)}{2}\) \(\sum_{k=1}^n k^2 = 1^2 + 2^2 + 3^2 + \dots + n^2 = \frac{n \cdot (n + 1) (2n + 1)}{6}\)

Let’s replace \(n\) with \(x\)

\[\frac{1}{3} \cdot \left( 4x^3 + 12x^2 + 11x \right) + 1 \\\]

This equation tells of the number of y blocks I need to build (x + 1) layer where x ≥ 0, x is Natural Number.

However, the problem is that in this case, I am not given with the number of layers I want to build. I am only given with the number of available blocks.

I thought it would be a good idea to find (x + 1) layer using the number of y blocks. Approximation (Secent line, Newton’s method, Gradient descent) would be a nice try.

 

Gradient descent

\[x_{n+1} = x_n - \eta \cdot \frac{d}{dx} \text{Loss Function}(x_n) \quad \text{where } \eta \text{ is the learning rate}\]

Define the loss function which I would like to minimize

\[\begin{align*} L(x) &= (\frac{1}{3} \cdot (4x^3 + 12x^2 + 11x) + 1 - y)^2\\ \frac{d}{dx} L(x) &= 2 \cdot (\frac{4}{3}x^3 + 4x^2 + \frac{11}{3}x + 1 - y) \cdot (4x^2 + 8x + 11x)\\ \end{align*}\]

However, I noticed that it does not work well because of learning rate…

 

Newton’s method

Newton’s method is similar to Secent line method, but Newton’s method requires deriviate

\[\begin{align*} x_{n+1} &= x_n - \frac{f(x_n)}{f'(x_n)} && \text{Newton's method}\tag 1\\ f(x_n) &= \frac{4}{3}x^3 + 4x^2 + \frac{11}{3}x + 1 - y \quad && \text{where y is given in the question} \tag 2\\ f'(x_n) &= 4x^2 + 8x + 11x \tag 3\\ x_{n+1} &= x_n - \frac{\frac{4}{3}x^3 + 4x^2 + \frac{11}{3}x + 1 - y}{4x^2 + 8x + 11x} && \text{$(2)$ and $(3)$} \end{align*}\]

For this method, I need to guess a good initial x value with the given y.

I can start with \(x_0 = \sqrt(\sqrt(y))\), which gives me the number very close to the x value I am trying to find.

Iterate the equation until the fraction becomes close to \(0\).

Code

Click here for Simple code 
#include <iostream>
int main()
{
  // number of blocks given
  int y;
  std::cin >> y;

  int layer = 0, sum = 0, odd = 1;
  while (sum < y)
  {
      int tmp = odd*odd;

      // check if adding the next layer will exceed the limit
      if (sum + tmp <= y)
      {
          sum += tmp;
          layer++;
          odd += 2;
      }
      else
      {
          break;
      }
  }
  std::cout << layer << std::endl;
  return 0;
}
Click here for Newton’s method code 
#include <iostream>
#include <cmath>
using namespace std;
int main() {

    int y;
    std::cin >> y;
    float x = sqrt(sqrt(y));

    // define f(x)
    double f = (4.0/3.0)*pow(x, 3) + 4*pow(x, 2) + (11.0/3.0)*x + 1.0 - y;
    double f_dx;

    // int i = 0;
    while (abs(f) > 0.0001) {
        f = (4.0 / 3.0) * pow(x, 3) + 4.0 * pow(x, 2) + (11.0 / 3.0) * x + 1.0 - y;
        f_dx = 4.0 * pow(x, 2) + 8.0 * x - (11.0 / 3.0);
        x = x - f / f_dx;
        // i++;
    }

    double nearest_integer = round(x);
    // Define a tolerance for when to floor
    if (abs(x - nearest_integer) >= 0.0001) {
        x = floor(x);
    }
    cout << x + 1 << endl;
    return 0;
}